Apresentaremos uma sequência didática sobre funções quadráticas com auxílio do GeoGebra, é muito importante a elaboração de uma sequência didática cujo p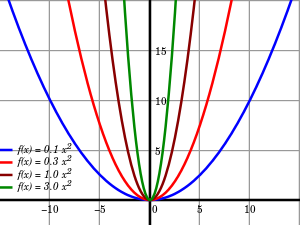
rofessor organize tal processo, podendo assim fazer modificações para adaptar, quando necessário, para melhor atender às necessidades de seus alunos. Essas aulas já devem ser apresentadas com o GeoGebra para familiarizar os estudantes com o programa. As atividades também são planejadas com exemplos práticos, relacionados com o cotidiano dos alunos, e com resoluções de problemas, a partir de sequências executadas pelos alunos no software.
O programa dispõe de duas janelas, a Janela Algébrica, onde acompanhamos as expressões que estão sendo trabalhadas e a Janela Gráfica, onde vemos os resultados gráficos. Também há várias ferramentas geométricas que auxiliam na construção e na transformação de gráficos que, por consequência, são apresentados na Janela Algébrica. Todas essas ferramentas são de fácil manuseio, não necessitam uma apresentação mais aprofundada, na prática, as atividades propostas já podem ser desenvolvidas.
Sobre as Funções Quadráticas, o matemático Iezzi (2013, p. 137) considera que: “Uma aplicação de f de R em R recebe o nome de Função Quadrática ou do 2º Grau quando associa a cada x ∈ R o elemento (ax^2+ bx +c) ∈ R, em que a, b e c são números reais dados e a ≠ 0. f(x) = ax^2+ bx +c (a ≠ 0). ”
Além da parte algébrica da função, é importante saber como ela é representada geometricamente, o gráfico de uma Função Quadrática é uma Parábola, uma curva aberta específica formada por pontos no plano cartesiano, considerando os valores de a na função, pode ter sua concavidade para cima ou para baixo. Toda parábola tem um ponto especial chamado de Vértice, ponto onde a função atinge valor Máximo ou Mínimo dependendo da concavidade. Como explica Iezzi (2013, p.139.): “A parábola representativa da função quadrática y = ax² + bx + c pode ter uma concavidade voltada para ‘cima’ ou para ‘baixo’. Se a > 0 a concavidade da parábola é para cima. Se a < 0 a concavidade é voltada para baixo.”
Dadas tais definições, somos levados a aplicar Funções Quadráticas usando o software GeoGebra e, para isso, vamos utilizar a ferramenta Controle Deslizante que possibilita alterar as variáveis da função. Configuramos os controles deslizantes com as seguintes opções: nome a, min. -5, max. +5 e incremento 0,1.